Recursion is the process of repeating items in a self-similar way. Any function which calls itself is called recursive. A recursive method solves a problem by calling a copy of itself to work on a minor issue. This is called the recursion step. Recursion is a valuable technique borrowed from mathematics. Recursive code is generally shorter & easier to write than iterative code. For example, sort, search & traversal problems often have simple recursive solutions.
Before diving into the sea, we all have to understand two statements –
A recursive function performs a task in part by calling itself to perform the subtasks. So, at some point, the process encounters a subtask that it can perform without calling itself.
- Base Case: This case, where the function doesn’t recur, is called the Base case.
- Cursive Case: The function calls itself to perform a subtask and is called the Cursive case.
For example, consider the factorial function: n! is the product of all integers between n and 1. The definition of recursive factorial looks like this:
n! = 1, (if n = 0)
n! = n * (n-1)! (If n>0)
In the recursive case, when n is greater than 1, the function calls itself to determine the value of (n –1)! and multiplies that with n. In the base case, when n is 0 or 1, the function returns 1.
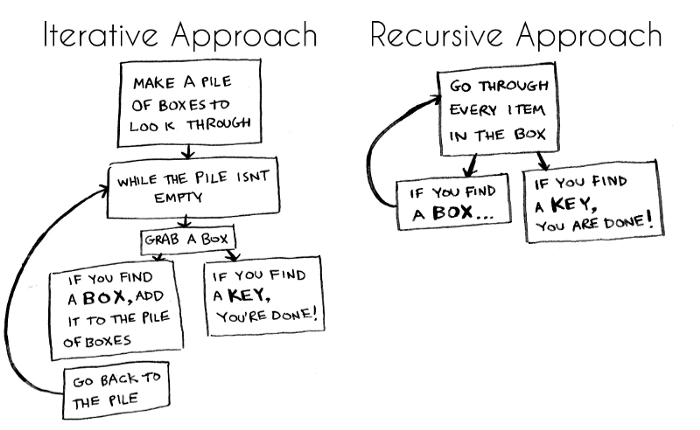
Recursion Vs. Iteration
The main inspiration comes to my mind before writing this blog is, which way is better? — Iteration or Recursion. From my point of view, the answer to this question depends on what we are trying to solve. A recursive approach mirrors the problem that we are trying to solve. A recursive approach mat makes it simpler to solve a problem but adds overhead for each recursive call.
Recursion
- Terminates when a base case is reached.
- Each recursive call requires extra space on the stack frame (memory).
- If we get infinite recursion, the program may run out of memory and result in a stack overflow.
- Solutions to some problems are easier to formulate recursively.
Iteration
- Terminates when a condition is proven to be false.
- Each iteration does not require any extra space.
- An infinite loop could loop forever since there is no extra memory being created.
- Iterative solutions to a problem may not always be as apparent as a recursive solutions.
Before compiling the whole discussion, there are some points worth mentioning:
- Recursive algorithms have two types of cases, recursive cases & base cases.
- Every recursive function case must terminate at a base case.
- Generally, iterative solutions are more efficient than recursive solutions
- A recursive algorithm can be implemented without recursive function calls using a stack, but it’s usually more trouble than it’s worth. That means any problem that can solve recursively can also be solved iteratively.
- Some problems are best suited for recursive solutions, while others are not.